Números reales
Los números reales son sólo números como:
Casi todos los números que se te ocurran son números reales
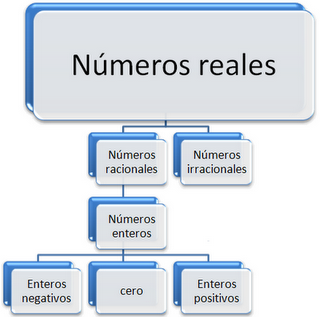
Los números reales incluyen:
| los numeros enteros (Como 1,2,3,4,-1, etc.) | |
| los numeros racionales (como 3/4, -0.125, 0.333..., 1.1, etc.) | |
| los numeros irracionales (como π, √3, etc.) |
Los números reales pueden ser positivos, negativos o cero.
Entonces... ¿qué números NO son reales?
| √-1 (la raíz cuadrada de menos 1) no es un número real, es un número imaginario | |
| Infinito no es un número real | |
| Y también hay otros números especiales que los matemáticos usan y que no son números reales | |
¿Por qué se llaman números "reales"?
Números Reales
Los números que se utilizan en el álgebra son los números reales.
Un número real es racional si se puede representar como cociente a/b, donde a sea un entero y b sea un entero no igual a cero. Los números racionales pueden escribirse en forma decimal.
Existen dos maneras:
* decimales terminales
* decimales que se repiten infinitamente
Los números reales que no pueden ser expresados en la forma a/b, donde a y b son enteros se llaman números irracionales. Los números irracionales no tienen decimales terminales ni decimales que se repiten infinitamente.
Orden de Operaciones
Reglas Importantes para Resolver Operaciones Aritméticas:
1. Primero resolver todo lo que esté dentro de simbolos de agrupación.
2. Evaluar las expresiones exponenciales.
3. Hacer todas las multiplicaciones y divisiones en orden de izquierda a derecha.
Ejemplo:
Propiedades de los Números Reales:
· Conmutativa de adición:
La conmutatividad implica que no importa el orden de operación, el resultado siempre es el mismo.
Por ejemplo:
4 + 2 = 2 + 4
· Conmutativa de multiplicación:
Por ejemplo:
4 . 2 = 2 . 4
· Asociativa de adición:
La asociatividad implica que no importa el orden en que se agrupe, el resultado es el mismo.
Por ejemplo:
(4 + 2) + 9 = 4 + (2 + 9)
· Asociativa de multiplicación:
Por ejemplo:
4 . (2 . 9) = (4 . 2) . 9
· Distributiva de multiplicación sobre adición:
Por ejemplo:
4 . (2 + 9) = 4 . 2 + 4 . 9
Reglas de los Signos:
1. En suma de números con signos iguales, se suman los números y el resultado lleva el mismo signo. Si los números tienen signos diferentes, se restan y el resultado lleva el signo del mayor.
Ejemplo:
5 + -8 = -3
2. En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.
Ejemplo:
5 - 8 = -3
5 - (-8) = 13
3. En multiplicación y división de números con signos iguales el resultado es positivo . Si los números son signos opuestos, el resultado es negativo.
Ejemplo:
5 x 8 = 40
5 x -8 = -40
Recta Numérica
Para construir una recta numérica, primero se escoge un punto en la recta que será un punto arbitrario al que le llamaremos cero (0). Este punto es llamado el origen de la recta numérica. El origen separa la recta en dos partes, el lado positivo y el lado negativo. A la derecha del origen está el lado positivo y el negativo está a la izquierda. En el lado derecho van números enteros positivos (en orden sucesivo) y en el lado izquierdo se escriben los números enteros negativos (en orden sucesivo), estos se marcan en unidades equidistantes.
Es importante recordar que para cualesquiera dos números reales diferentes a los que llamaremos a y b, siempre uno es mayor que el otro.
· Si a - b es positivo, entonces a > b.
· Si b - a es positivo, entonces a < b.
Valor Absoluto
La distancia de un número en la recta numérica desde cero (0) se llama valor absoluto. Se representa con elsímbolo |x|. El valor absoluto de un número se calcula de la siguiente manera:
· si el número es negativo, lo convertimos a positivo.· si el número es cero o positivo, se queda igual.
Ejemplos:
|7| = 7
|-7| = 7
Real no quiere decir que aparezcan en el mundo real
| No se llaman "reales" porque muestren valores de cosas | |
| En matemáticas nos gusta que los números sean puros y exactos, si escribimos 0.5 queremos decir exactamente una mitad, pero en el mundo real una mitad puede no ser exacta (prueba a cortar una manzana exactamente por la mitad | |
ACONTINUCION EL ENLACE O LIN PARA VIDEO PREPARADO SOBRE LOS NUMEROS REALES EN ANIMOTO.COM
link de video http://animoto.com/play/M058jtZiGq1Va4FyCYiGBw
video1
Create your own video slideshow at animoto.com.
vidoe 2
Create your own video slideshow at animoto.com.